When I was in college, I always thought about why we need connections and why they are so important in the steel structure. Now I have the answer to that. Because we can’t transport massive members in the field, it will make steel structures more costly. And the answer to why it is so important is when the members fails and connection is safe, we under utilized the members. So again, we are losing money.
In this article, we will discuss the bolted connections and different checks according to the IS 800:2007.
What are bolts?
To understand the bolted connection, you need to understand the bolt first. You see, in the figure, it has two parts one is a bolt, and another is Nut. The bolt has two part shank and a threaded portion.
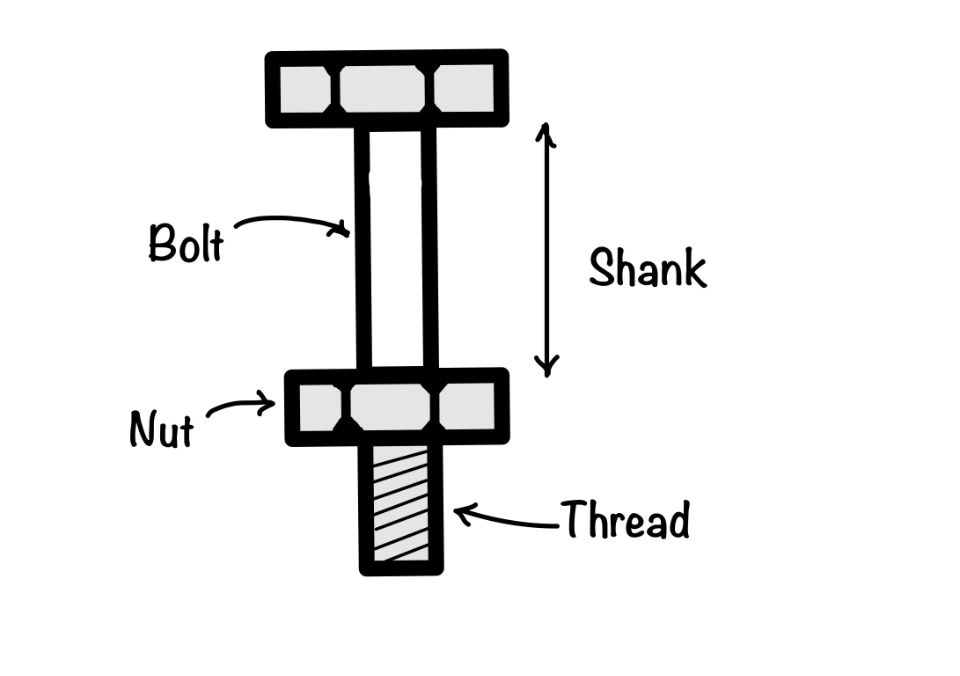
There are two types of bolted connections. One is a black bolt of bearing type connection, and the other is friction grip bolts. In this article, we will learn about friction grip bolts.
According to IS code, we refer to the bolts as a grade of bolt. Like M 4.6 means the bolt has an ultimate shear strength of 400 MPa, and the yield strength of the bolt can be calculated as $0.6 \times 400 =240$ MPa.
What are the different terminologies used in the bolted connections?
Before the connection design, we need to learn some basic terminologies we use in the steel design. These terminologies are essential because IS code or, say, any standard reference manual uses these terminologies.
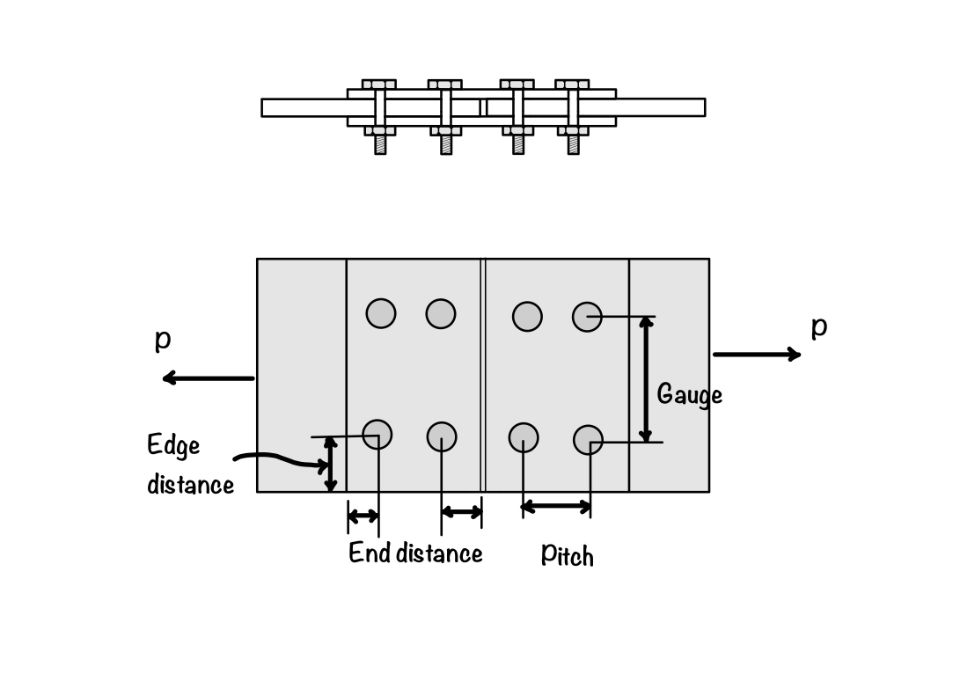
The important terminologies in the steel structures are as follows:
- Pitch: It is the center-to-center distance between the two bolts measured in the direction parallel to the direction of load applied. For a clear understanding, please refer figure.
- Gauge: It is the center-to-center distance between the two bolts measured perpendicular to the direction of load applied.
- Edge distance: It is the distance measured from the center of the last bolt to the edge of the plate. Edge distance is measured parallel to the direction of the load applied.
- End distance: It is the distance measured from the center of the last bolt to the edge of the plate. The end distance is measured perpendicular to the direction of the load applied.
- Net tensile area: When the critical section of the plate passes through the threaded portion of the bolt, the area used to bear the stress is critical stress. The net tensile area of the bolt is calculated as the $0.78 \times A_s$. Where $A_s$ is the gross area of the bolt.
What do we mean by bolt strength?
When we make the connection using the bolts, we need to find the strength of the connection. To do this, we need the strength of the bolt.
The strength of the bolt is defined as the stress it can take just before the failure of the bolt. So now the question comes to how to find the failure of the bolt.
The bearing-type bolts may fail in the following ways:
- Bearing failure: Bolts subjected to loads in the members may lead to failure by bearing. The figure below shows the bearing type failure.
- Shearing Failure: This type of failure occurs when two plates try to shear off the bolts. We will consider the cross-sectional area of the bolt to calculate the shear strength of the bolt.
- Tension failure: When bolts resist the tension load, as shown in the figure, the tension may lead to failure. The net section of the bolt is used to calculate the tension capacity of the bolt.
We will calculate the strength for all kinds of possible failure, and the minimum is used as bolt strength.
How to find the strength of a bolt in shear?
Now after discussing the overview of bolt strength, we will find the strength of the bolt in shear. IS code suggests the following formula to determine the design shear strength of bolt $V_{dsb}$ in the shear.
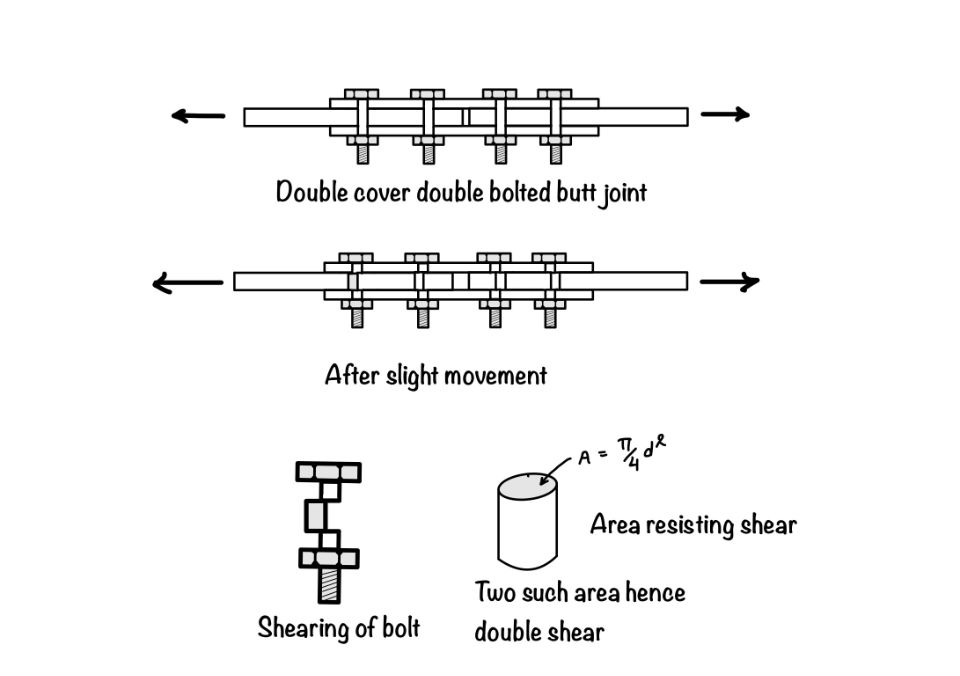
$$ V_{dsb}=\frac{V_{nsb}}{\gamma_{mb}}=\frac{f_{ub}}{\sqrt{3}\gamma_{mb}}(n_nA_n+n_sA_s) $$
Where :
- $V_{dsb}$ is the design shear strength of the bolt.
- $V_{nsb}$ is the nominal shear strength of the bolt.
- $f_{ub}$ is the ultimate strength of the bolt.
- $n_n$ is the number of sections passing through the threaded portion of the bolt.
- $n_s$ is the number of sections passing through the shank area of the bolt.
- $A_s$ is the shank area or gross area of the bolt. It can be calculated from the $\frac{\pi}{4}d^2$, where $d$ is the diameter of the bolt.
- $A_n$ is the net area of the bolt. This can be calculated from the thread data. In the absence of such data, IS code suggests $A_n=0.78\times A_s$ for the calculation of the net tensile area of the bolt.
- $\frac{1}{\sqrt{3}}$ factor comes from the stress transformation theory, which we have discussed in a previous article.
We use the above formula to calculate the shear strength of the bolt.
How to calculate the bearing strength of the bolt?
We can calculate the bearing capacity of the bolt by using the IS code formula. IS code in clause 10.3.1 discuss the bearing strength of the bolt.
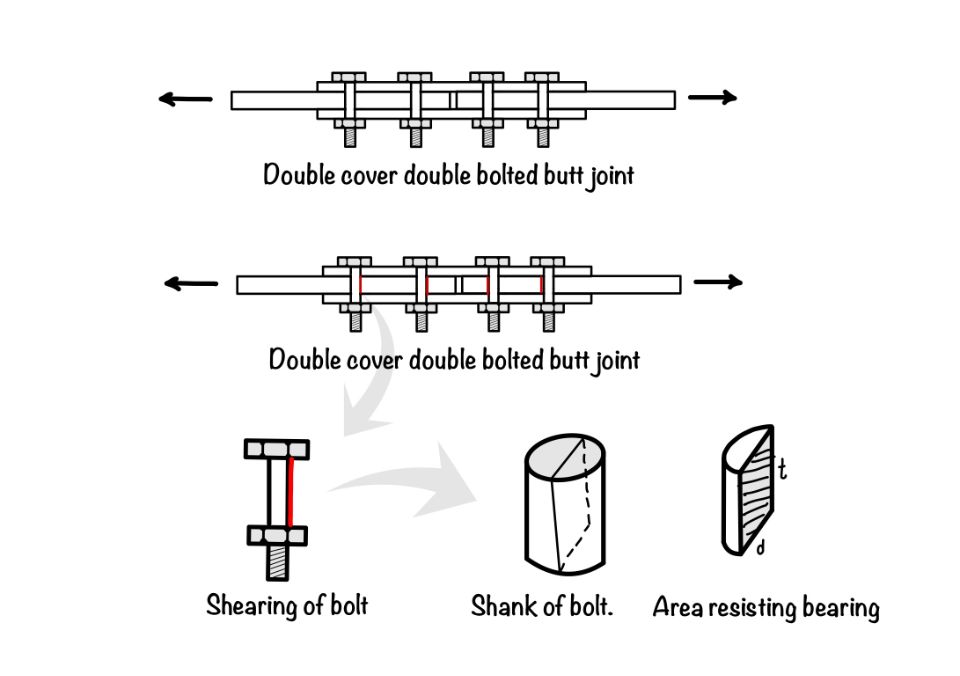
$$ V_{dpb}=\frac{V_{npb}}{\gamma_{mb}}= 2.5k_b (dt)f_u\\ k_b=\min\left\{\frac{e}{3d_0},\frac{p}{3d_0}-0.25,1,\frac{f_{ub}}{f_u}\right\} $$
Where:
- $V_{dpb}$ is the design bearing strength of the bolt.
- $V_{npb}$ is the nominal bearing strength of the bolt.
- $\gamma_{mb}$ is the partial safety factor for the material of the bolt.
- $d$ is the diameter of the bolt.
- $t$ is the thickness of the thinner plate.
- $f_u$ is the ultimate strength of the plate.
- $f_{ub}$ is the ultimate strength of the bolt.
- $e$ is the edge distance of the connection.
- $p$ is the pitch distance of the connection.
- $d_0$ is the diameter of the whole. This can be calculated from Table 19 of IS800:2007.
How to find the tensile strength of the bolted connection?
$$ T_{db}=\frac{T_{nb}}{\gamma_{mb}}= \min\left\{0.9A_nf_{ub},\frac{f_{yb}A_{sb} \gamma_{m1}}{\gamma_{m}} \right\} $$
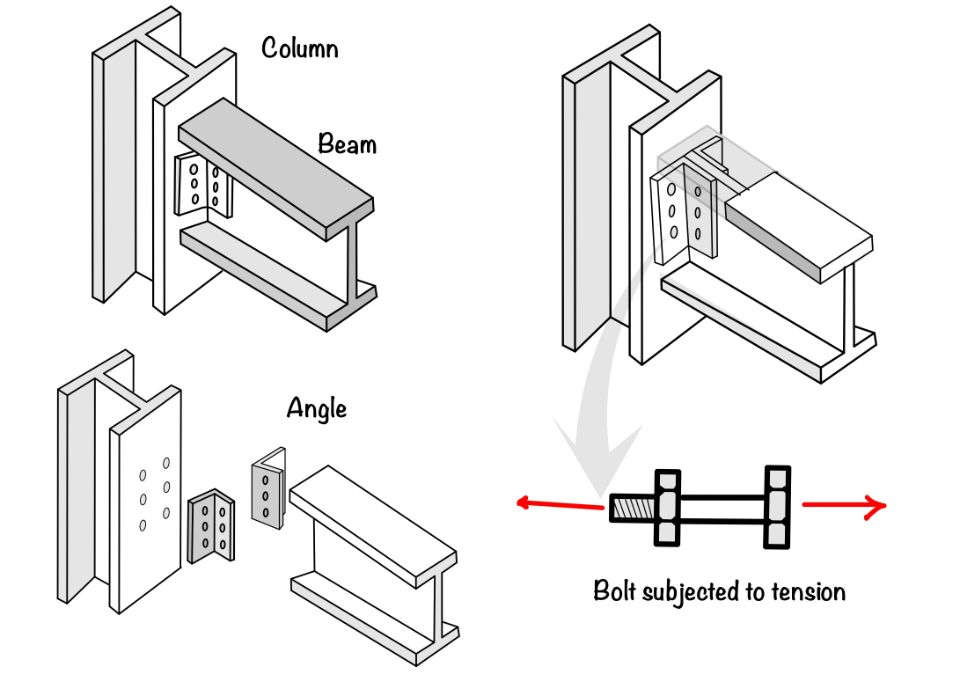
Where:
- $T_{db}$ is the design tension capacity of the bolt.
- $T_{nb}$ is the nominal tension capacity of the bolt.
- $\gamma_{mb}$ is the partial safety factor for the bolt material.
- $A_n$ net tensile area as specified in the IS1367. Where a tensile area is not given, the net tensile area is taken as the area at the root of the threads.
- $A_{sb}$ is the shank area of the bolt.
What happens when tensile and shear forces are acting simultaneously in the bolted connection?
When a bolt is in the tensile and shear force simultaneously, which is a persistent case. We have to check the following condition to ensure the bolt is safe.
$$ \left\{\frac{V_{sb}}{V_{db}}\right\}^2+\left\{\frac{T_b}{T_{db}}\right\}^2\le 1 $$
where:
- $V_{sb}$ is the shear force in the bolt.
- $V_{db}$ is the design shear strength of the bolt.
- $T_b$ is the tension force in the bolt.
- $T_{db}$ is the design tension capacity of the bolt.
Example of the bolted connection
To explain the process of the above-discussed clause, we will solve one design problem to completely understand this issue.
Suppose you want to design the connection with a bolt of 20 mm diameter of grade 4.6. You will be given three different cases. First, you have to find out the strength of the bolt. The main plate which we need to join has a 12 mm thickness and the ultimate strength of the plate is $410$ MPa.
For the first case, you have the lap joint.
Please see the figure to understand the philosophy of strength determination of the bolt.
As we can see in the figure, the bolt is in the single shear and the bearing. So you have to check the strength for these two cases, and the minimum of the two will be the strength of the bolt.
Strength determination in the lap joint.
We have the following data given in the question:
$f_u$ – 410 MPa, $f_{ub}$ =400 MPa, $\gamma_{mb}$ = 1.25, $A_{nb}=0.78 \times A_{sb}$ = 245 ${\mathrm{mm}}^2$.
From clause 10.3.3 of IS 800:2007, we can find the formula for shear strength.
$$ V_{dsb}=\frac{V_{nsb}}{\gamma_{mb}}=\frac{f_{ub}}{\sqrt{3}\gamma_{mb}}(n_nA_n+n_sA_s) $$
Substituting the value of the from the question
$$ V_{dsb}=245\times \frac{400\times 10^{-3}}{\sqrt{3}\times 1.25}= 45.26 kN $$
The strength of the bolt in the bearing
$$ V_{dpb}=\frac{V_{npb}}{\gamma_{mb}}= 2.5k_b (dt)f_u\\ k_b=\min\left\{\frac{e}{3d_0},\frac{p}{3d_0}-0.25,1,\frac{f_{ub}}{f_u}\right\} $$
Substituting the values as follows:
for 20 mm diameter bolt $d_0$ =22 mm and $e = 33$ mm. (For rolled edge)
Assume the pitch of the bolt = $50$ mm.
$$k_b=\min\left\{\frac{33}{3\times 22}=0.5, \frac{50}{3\times 22}-0.25= 0.5, 1,\frac{410}{400}\right\}\\k_b=0.5$$
$$V_{dpb}=2.5 \times 0.5 \times \frac{410}{1.25}\times (20\times 12)=98.4 kN$$
Hence, you must select the bolt’s minimum shearing and bearing strength. Strength is 45.26 kN.
How to find the strength in the butt joint.
For the same plate material and bolts, now you have to check the strength for the single cover butt joint, the cover plate being 10 mm thick.
You can take the given data from the previous section. Now see the figure for more visualization of the connection.
The bolt will be in single shear and bearing. Therefore, we will consider the thickness for the bearing will be the least of the aggregate thickness of the cover plates and the minimum thickness of the main plates jointed.
Hence, t=10 mm. The shear strength in the bolt will be the same as we have calculated in the previous section.
$$ V_{dsb}=45.26 kN $$
The strength of the bolt in bearing,
$$ V_{dpb}=\frac{V_{npb}}{\gamma_{mb}}= 2.5k_b (dt)f_u\\ k_b=\min\left\{\frac{e}{3d_0},\frac{p}{3d_0}-0.25,1,\frac{f_{ub}}{f_u}\right\} $$
$$ V_{dpb}=2.5\times 0.5 \times 20 \times 10 \times \frac{410}{1.25}\times 10^{-3}= 82.0 kN. $$
The strength of the bolt will be the minimum of the strength in shear and bearing and is $45.26$ kN.
Conclusion
In this article, you have learned the following key points.
- Pitch: It is the center-to-center distance between two bolts measured in the direction perpendicular to the applied load.
- Gauge: It is the center-to-center distance between two bolts measured in the direction parallel to the applied load.
- Shear strength: It is the bolt’s stress just before the bolt’s shear failure.
- Bearing strength: It is the bolt’s stress just before the bolt’s bearing failure.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author

This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


