When you push or pull on something, like a beam or a shaft, it doesn’t just bend or twist—it usually does both at the same time. We call this “combined stress.” Imagine lifting a bag: your hand not only moves up but might also twist a bit.
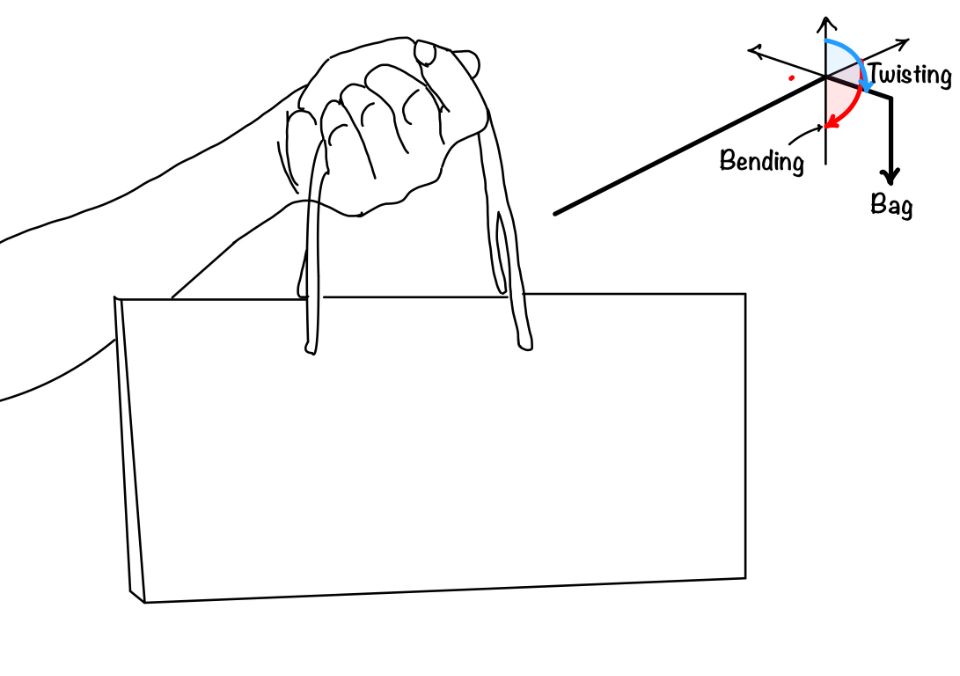
In our previous discussions, we looked at bending and twisting separately, but in real life, they often happen together. Engineers need to consider both when designing things like bridges or machines, making sure they can handle the mix of forces without breaking. It’s like solving a puzzle to keep everything stable and safe.
Stress due to pure bending
If you will apply the load in such a way that it will create the pure bending in the beam. In such situations we can find the stress in the beam using the following formula:
$$\frac{M}{I} =\frac{\sigma}{y}= \frac{E}{R} $$
Where: $M$ is bending moment at that section, $I$ is the moment of inertia about the $Z$ axis, $\sigma$ is the stress at location $y$ of the beam, $E$ is the elastic modulus of the beam and $R$ is the radius of curvature.
You can find the full derivation for the bending stress in the article bending stress of the beam.
Stress due to torsion in the beam
If you apply the pure torque in the beam. This will create the shear stress in the section of the beam as shown in the figure. We can use the following formula to determine the stress due the applied torsion:
$$ \frac{T}{J}=\frac{\tau}{r}=\frac{G\theta}{l} $$
Where: $T$ is the torsion in that section where we are supposed to find the shear stress $\tau$ due to torsion at distance $r$ from the centre of the beam. $J$ is the polar moment of inertia and $G$ is the shear modulus of elasticity or modulus of rigidity and $\theta$ is angle of torsion and $l$ is the length of shaft.
For the full derivation of the pure torsion formula you can refer the detailed article torsion.
What happens when both acts simultaneously
In the practical situation where the bending and torsion forces are acting simultaneously we need to apply the superposition. For clear understanding please play with the widget given below. In this case the force is causing bending and torsion and we can see the stress condition due to this at the extreme fibre of the beam. The tensile stress $\sigma_x$ is due to the bending moment and the shear stress $\tau_{xy}$ is due to the torsion effect of the beam. For more understanding you can use the widget. $e$ is the eccentricity of the load. You keep on increasing the eccentricity it will increase the bending moment in the beam. The magnitude of the torsion applied on the beam depends on the lever arm $l$. You can also increase of decrease this by changing the $l$ .
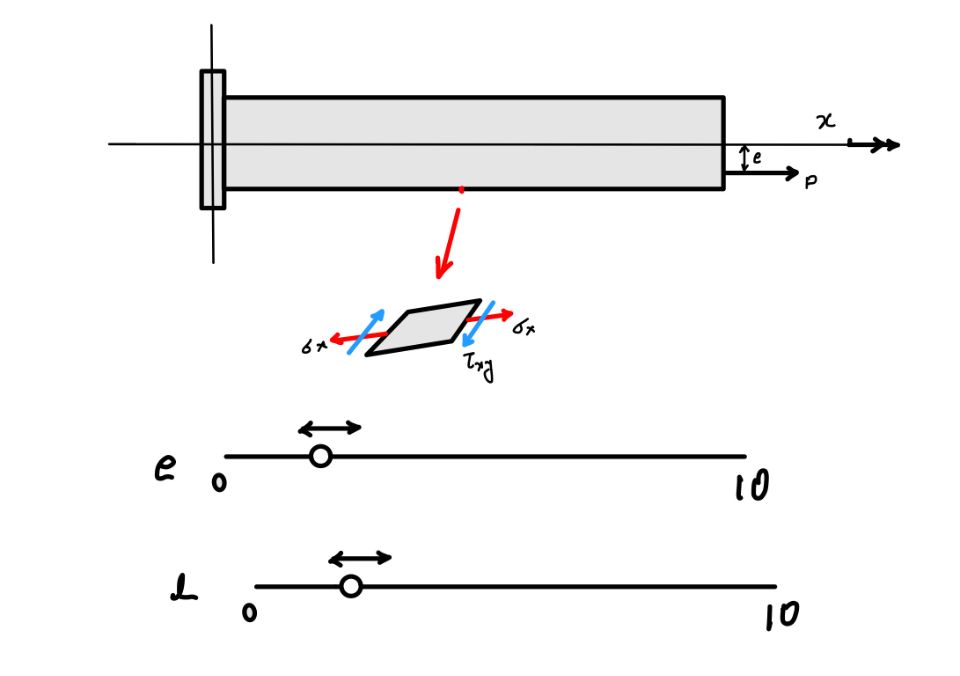
When you keep $e$ equal to zero only torsion is acting hence the tensile stress $\sigma_x$ will be equal to zero. When you keep $l$ equal to zero only bending moment will be acting on the beam hence shear stress $\tau_{xy}$ will be equal to zero.
Limitations
The above formulation is valid in the following circumstances:
- Superposition: We have used the superposition while discussing the above concepts. And superposition is valid upto only proportional limit. Hence where stress and strain relation is non linear the above concept will not work.
- Isotropic and homogenous: We have discussed while discussing the bending stress and torsional stress in different articles material should be homogenous and isotropic. Hence above formulation is valid for the isotropic and homogenous materials.
- No warping: We have assumed that because of bending and torsion there is no warping in the section and hence they produce the linear stresses.
finding the maximum stress at that point
Finding the stress for the combined loading is the need of practical situation. In real world you will never find the loading is isolation they always comes in combination. To apply the concept to real life this article is very helpful.
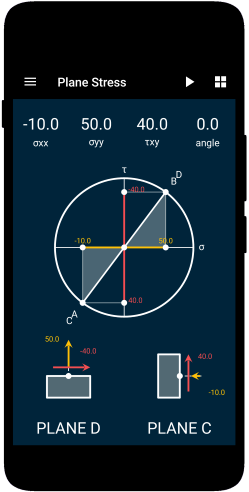
To find the maximum stress at the point $P$ due to the stress condition as we have discussed above we can use Mohr’s circle. You can use our Solid Mechanics app to find out the principle stresses as shown in the figure.
Conclusion
This article explains you how you can apply the theoretical concepts you have learned. This article explains the situation when the bending stress and torsional stress comes simultaneously in the beam.
In this blog you have learned following things:
- Superposition: When the torsion and bending both acts we can add them one by one. This is called superposition theorem.
- Stress due to bending: Bending in the beam create tensile stress in the bottom section of the beam in this particular case. It may be either compression stress or tension stress depending upon the location of point and nature of load.
- Stress due to torsion: Torsion caused the shear stress in the beam. Again on the location of point and nature of torque shear stress may be positive or negative.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


