We designed the one-way slab in the previous article. In this article, we will design the same one-way slab through the RCC Slab Design App. The Eigenplus team made this App.
This App has the following features:
- User friendly: Useful RCC Slab Design App with clean and intuitive user interface.
- Complete solution: RCC Slab Design is a free app for designing one-way and two-way reinforced concrete slab systems as per Indian Standards.
- Boundary conditions: Ten different boundary conditions are there for which we can perform RCC Design and detailing.
- Save project: Option to save the design projects in local storage.
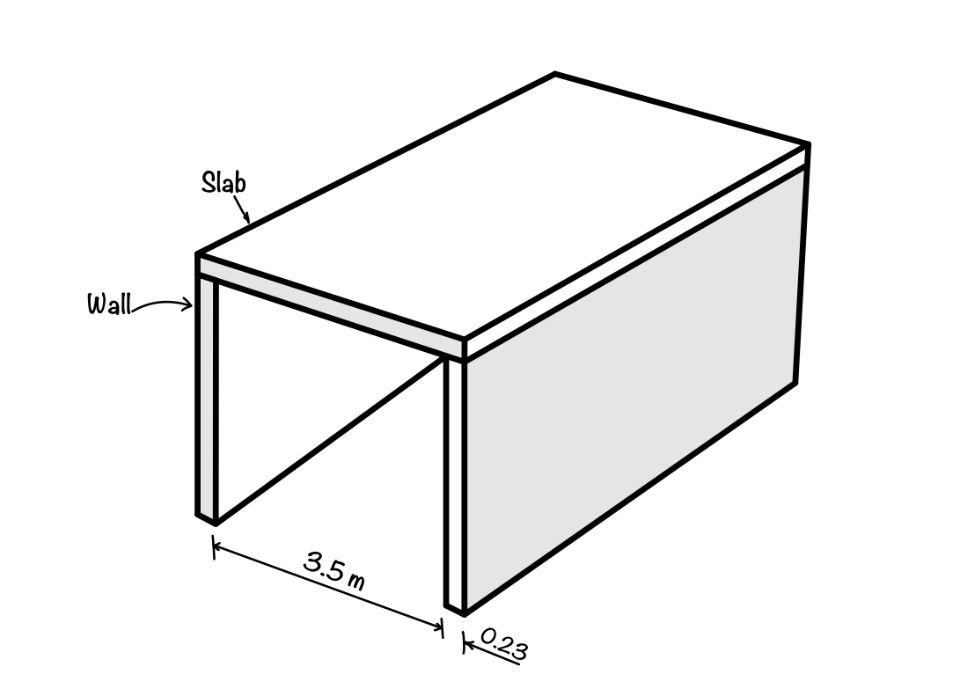
Problem statement for Slab App
The slab has a clear span of 3.5 m and is subjected to a live load of 3.5 kN/m2 and a floor load of 1.5 kN/m2. The supporting wall has a width of 0.23 m. For our design calculations, we will assume M20 concrete and Fe415 steel, commonly used materials in construction.
Detailing and input data in the Slab App
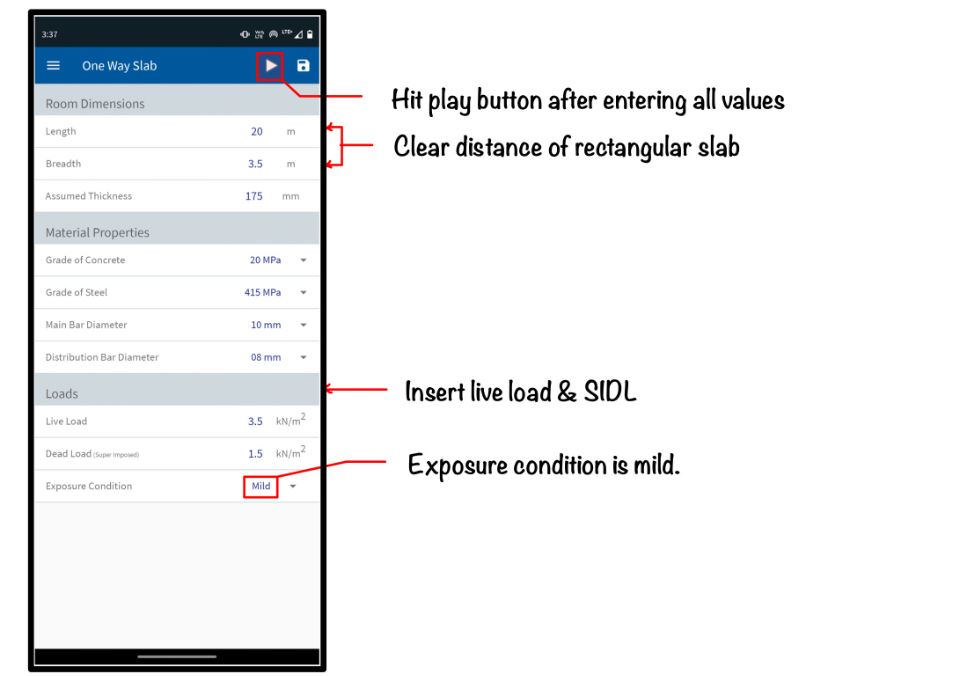
In this section, we will see what input data is required in the Slab App to design the one-way slab. As shown in the figure enter the clear distance of the rectangular slab. Here these values are as follows:
- Length = 20 m
- Breadth = 3.5 m
- Assumed Thickness = 175 mm (We considered by $L/20$)
After entering the dimension of the slab we need to enter the material properties of the slab. Here the grade of concrete is 20MPa and the grade of steel is 415 MPa.
After entering the grades of steel and concrete we need to enter the diameter of the main reinforcement and the distribution reinforcement. Here diameter of the main bar is 10 mm and the distribution bar is 8 mm.
After entering all these properties we need to enter the loads on the slab. The live load on the slab is $3.5 kN/m^2$ and the superimposed dead load is $1.5 kN/m^2$. Then App asks for the exposure condition. Here we are entering the exposure condition as mild.
After entering all the data now hit the play button as shown in the figure.
Calculation of initial dimension and loading in Slab App
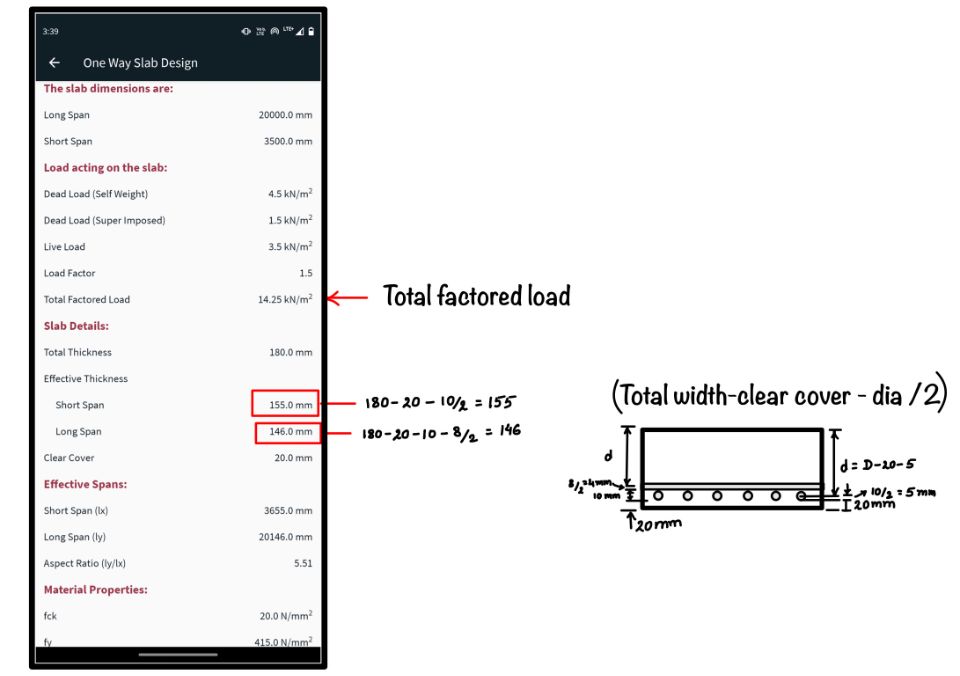
After hitting the play button in the Slab App the following screen appears as shown in the figure. The load in the slab is now calculated which will be used for the moment calculation in the slab.
The details of the effective thickness calculation are shown in the figure. After calculating the effective thickness of the slab the effective span of the slab is shown in the App. These effective spans are used to calculate the design moment in the slab.
Calculation of reinforcements
After calculating the effective span of the slab and the factored load of the slab we calculate the design moment. The design moment in the slab is $23.8 kNm$. The detailed calculations and verification 0f results we can do from the earlier article.
After the calculation of the design moment in the next section, the app gives spacing of reinforcement. After the main bar calculation, the distribution reinforcement is shown. This calculation is based on the gross area of the slab which is 1,80,000 $mm^2$.
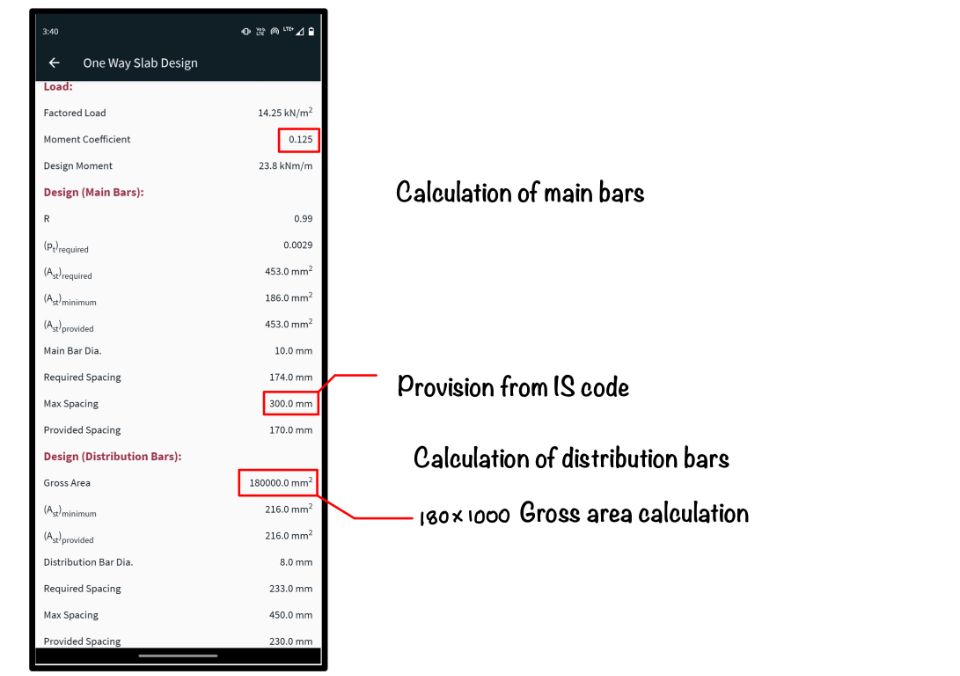
The final result is the spacing of the main and distribution reinforcement. This App presents the result in the last line with red colour.
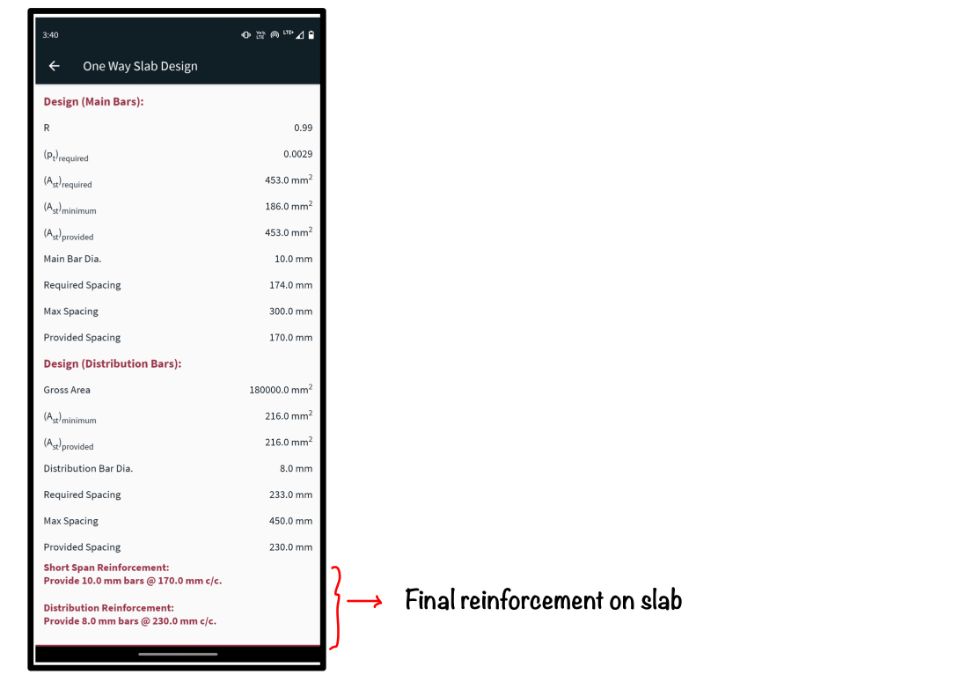
Conclusion
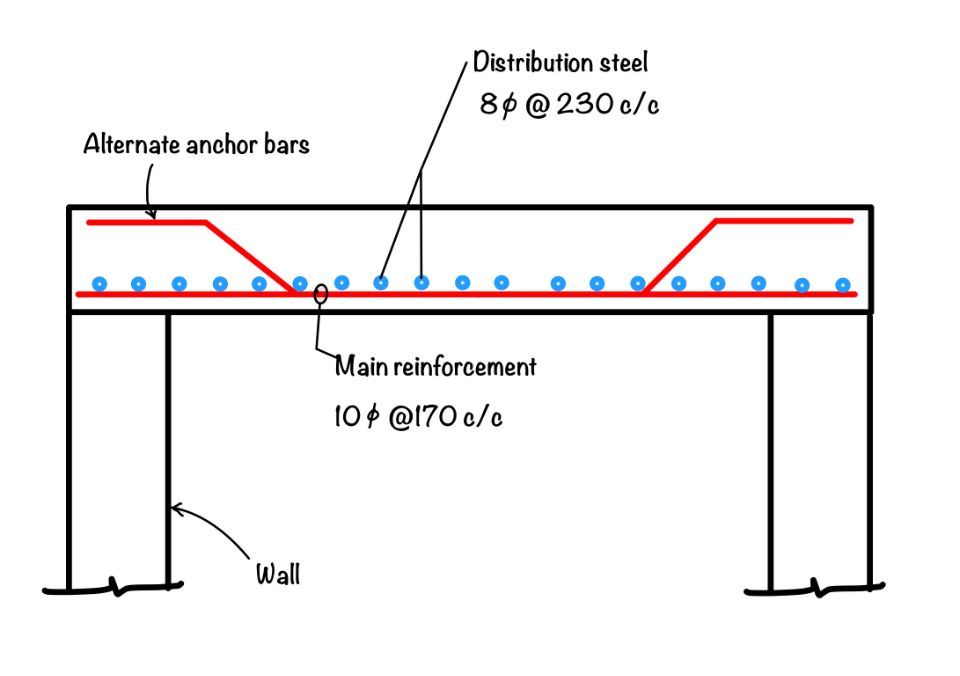
We presented the final drawing as shown in the figure. The final result is the same as obtained from the manual calculation in the previous article.
We have learned the following key points from this article:
- Efficiency: The Slab App is efficient and clean. The user enters data without any confusion.
- Dependency: The Slab App is dependable. As this article compares the results from the manual calculations and App calculations.
Slab design
- RCC Slab Design is a free app for designing one way and two way reinforced concrete slab systems as per Indian Standards.
- RCC Design and detailing could be performed for ten different boundary conditions specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.

This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


