Designing two way slabs: An example

A two-way slab is a type of R.C.C. slab that distributes loads in two perpendicular directions efficiently. The term "two-way" is to describe the bending behavior of the slab in both directions, which provides structural stability and strength. The primary characteristic of a two-way slab is its ability to transfer loads through flexural action in two orthogonal directions. This is achieved by incorporating a grid of reinforcement bars in both the longitudinal and transverse directions. The reinforcement bars resist bending moments and distribute the applied loads across the slab's entire area.

The design of a two-way slab involves considerations such as load distribution, moment redistribution, shear forces, and deflection limits. IS codes provide guidelines and formulas for determining slab thickness, reinforcement layout, and detailing to ensure strength and stability.

In this blog, we aim to explore the design process of two-way slabs, offering practical insights and a step-by-step example. Whether you're an experienced professional or an aspiring engineer, this resource emphasizes the significance of following design codes and provides practical guidance for effectively implementing two-way slabs.

We will walk through the detailed design process of a simply supported two-way slab with specific parameters.

Design of R.C.C slab for a room of clear dimension 4m*5.5m. The slab is supported on monolithically casted beam all-around of width 230mm. Assume live load of 3 kN/m2 and a floor load of 1.5 kN/m2. Use M25 concrete and Fe415 steel.

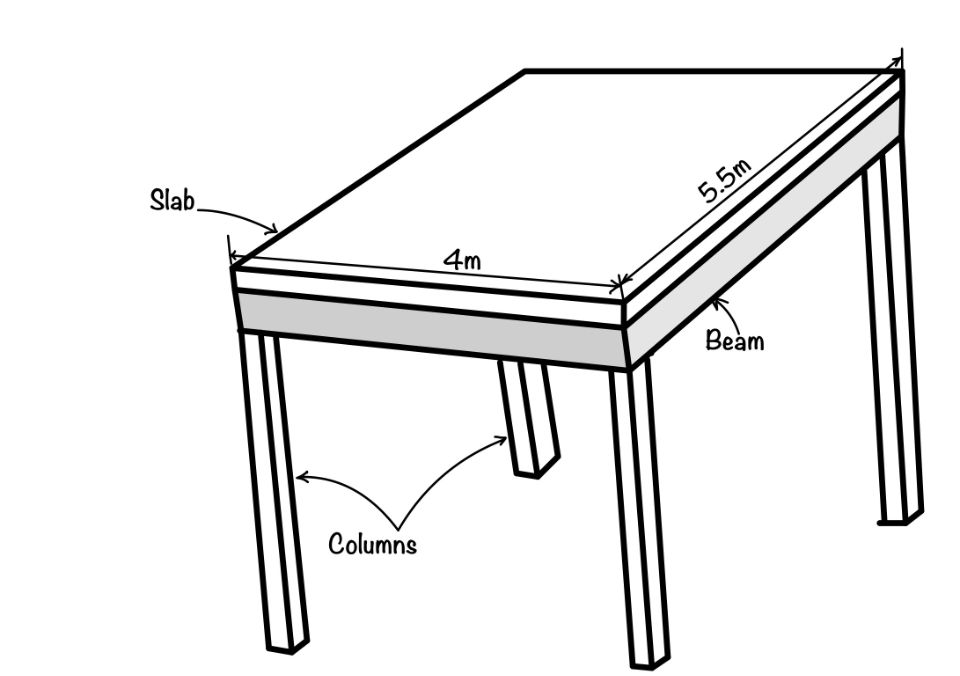
Check this post to learn the detailed step by step procedure of two way slab.

1. Check the aspect ratio

$\frac{\text{Longer span}}{\text{Shorter span}} = \frac{5.5}{4} = 1.375 < 2$

since, the ratio is less than 2, so design it as two way slab.

2. Trial depth as per the serviceability condition

Assume, $\frac{\text{Shorter span}}{\text{Effective depth}} = 30$

$d = \frac{4000}{30} = 133.33 mm$

so, lets assume d = 133 mm

Now, overall depth of slab = d + clear cover + half dia of bar

$D = 133 + 15 + 5 = 153 mm$; Assume D = 150 mm

So, effective depth = 150 - 15 - 5 = 130 mm

3. Calculate the effective span, as per IS 456: 2000.

Effective span is taken as lesser of two ;

1. Center to center of supports or clear span + width of support $L = 4 + 0.23 = 4.23 m$

2. Clear span + effective depth of slab $L = 4 + 0.13 = 4.13 m$ or $L = 5.5 + (0.13-0.01) = 5.62 m$

So, take effective span as 4.13 m and 5.62 m.

4. Calculation of Loads

Consider the various loads due to

• Self weight: Self load refers to the weight of the structure itself, including the weight of the material used in construction and any fixtures or furnishings $Self weight = 0.150 \times 25 = 3.75 kN/m$

• Dead Load: To refer to the permanent and stationary weight of a structure and its components. $Dead load = 1.5 kN/m$

• Live load: The temporary or movable loads that a structure or building is prone to during its use or occupancy. $Live load = 3 kN/m$

• Total load : Calculate the total load and factored load (1.5 * Total load) $Total load = W_u = 12.375 kN/m$

5. Calculation of factored bending moment

Aspect ration = longer effective span / shorter effective span = 5.62/ 4.13 = 1.36. Take 1.5 for simplify your calculation.
Compute the factored bending moment, using the value of coefficient bending moment from Table 26 of IS 456: 2000.

The formulas are generalized in the Indian standard code:

$M_{x} = \alpha_x \times w_x \times l_x^2$

$M_{y} = \alpha_y \times w_y \times l_x^2$

	Mx (kN-m)	My (kN-m)
At support	= 0.075*12.375*4.132 = 15.83	= 0.047*12.375*4.132 = 9.92
At mid-span	= 0.056*12.375*4.132 = 11.82	= 0.035*12.375*4.132 = 7.39

6. Check for concrete Depth from Bending Moment criteria

$M_u = 0.138 f_{ck} bd^2$, $15.38e6 = 0.138 \times 25 \times 1000 \times d^2$, $d = 66.77 mm$ < 130 mm. OK.

7. Determine the area of reinforcement ( Ast )

Compute the value of Ast using the formula :

M_u = 0.87 f_y A_{st} \[d - f_y A_s /( f_{ck} b)\]

M_u = 0.87 \times 415 \times A_{st} \[ 130 - 415 \times A_{st}/ (25 \times 1000)\]

	Asx (mm2)	Asy (mm2)
At support	353.193	217.384
At mid span	260.494	160.746

According to IS 456:2000, the minimum percentage of steel for Fe 415 is 0.12 %, which is provided as distribution steel.
$\frac{0.12}{100} \times b d = 180 mm^2$

If we are using 10 mm dia. bars, then the spacing of the bars is computed using the:
$S = \frac{a_{st}}{A_{st}} \times 1000$

	Sx (mm)	Sy (mm)
At support	222	361
At mid span	302	436

The spacing of bar should be less than 3d or 300 mm.
Hence use 10 mm die bars c/c at the following spacing:

	Sx (mm)	Sy (mm)
At support	200	300
At mid span	300	300

Conclusions

In this blog post, we have delved into a practical problem that provides an explanation of a two-way slab. As per IS:456:2000, Indian Standards, we have designed a two-way beam section.

So, let us discuss the key points from this problem as follows:

• Significance of Design and Analysis: It gives the need to consider various factors, including load distribution, and reinforcement to ensure the function of a two-way slab.

• Consideration of Critical Factors: Throughout our design procedure, we have discussed significant factors such as bending moments, shear forces, and deflection limits.

• Integration of Theory and Practice: All in one, by following the reinforcement detailing guidelines as per Indian codes, engineers can develop structurally sound and efficient solutions that meet safety and performance criteria.