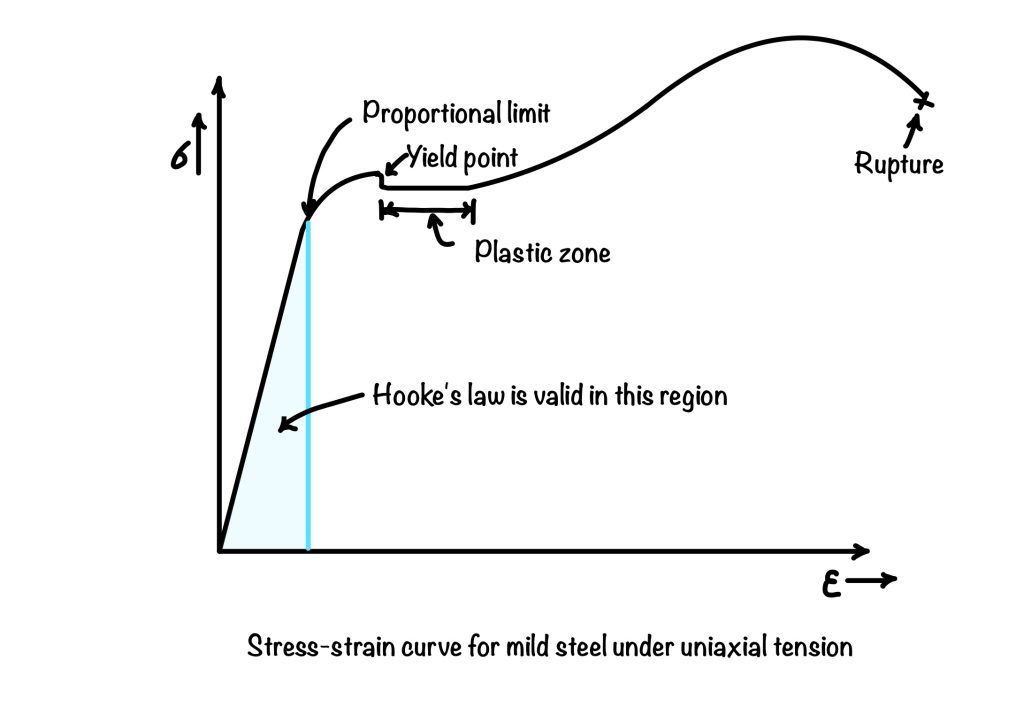
If you are looking for Hooke’s law, you must be familiar with the stress-strain behavior of the material. We plot the stress versus strain curve for the material to know its behavior under different loading conditions. This stress-strain curve has a small portion where the curve is straight, and Hooke’s law is defined on that area. This post will discuss Hooke’s law, its application, and the restrictions or assumptions considered while explaining it. After reading this post, you can calculate the elongation and shear deformation of the material subjected to axial tension and shearing force, respectively.
Definition of Hooke’s Law
As a formal definition, Hooke merely says stress is proportional to strain. However, in 1807, Thomas Young later introduced the constant of proportionality, known as Young’s modulus. For more clarity, let us consider the stress-strain curve for mild steel. The straight line portion is valid for Hooke’s Law in this curve.
$$ \sigma = E \varepsilon $$
Here E is Young’s modulus, later known with the phrase modulus of elasticity. From the above equation, you can find the units of modulus of elasticity are the same as units of stress, as strain is a dimensionless quantity. Like modulus of elasticity of steel in SI unit is approximately \(200 \times 10^9 N/mm^2 (200GPa)\). In US customary Units, the modulus of elasticity for steel is approximately \(29 \times 10^6 psi\).
Application of Hooke’s law (axial )
You can get the more convenient variation of Hooke’s law by replacing stress with \(P/A\) and replacing the strain with the \(\Delta L/L\).
$$ \frac{P}{A}=E\frac{\Delta L}{L} $$
$$ \Delta L = \frac{PL}{AE} $$
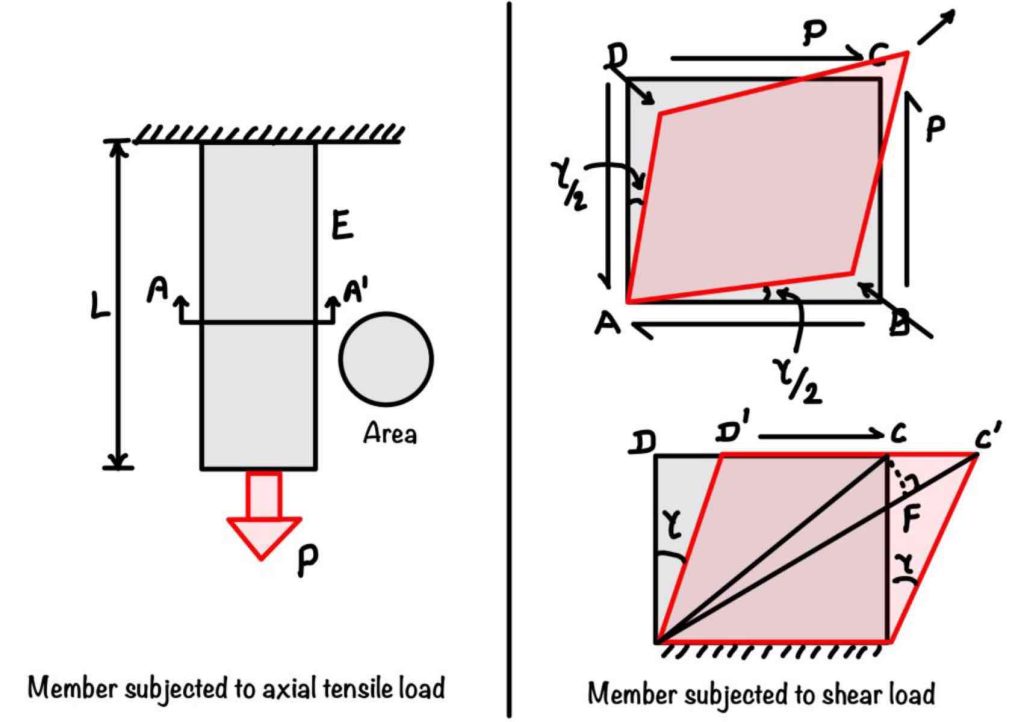
The above case is for a bar with the axial tensile load. One more interesting case is the shear force. When you will apply shear force in the body, it causes shearing deformation, just like axial force causes elongation.
Application of Hooke’s law (shear force)
You can see the shearing action in the figure. We can visualize the infinitesimal sliding of the infinitely thin layer as shown in Fig. This sliding gives the total shearing deformation \(\Delta_s\). Well, the phenomenon looks very simple, but this is more complex, which we will discuss in a separate blog post. For the present case, this is the behavior of shear force.
We can calculate the average shearing strain by dividing the \(\Delta_s \)by \(L\).
$$ \tan \gamma \approx \gamma = \frac{\Delta_s}{L} $$
More precisely, the shearing strain is the angular change between two perpendicular faces of a differential element. Now applying Hooke’s Law for shear force condition. The shear stress will be proportional to the shear strain produced, and the modulus of elasticity in shear will be the proportionality constant. This modulus of elasticity in shear is also known as the modulus of rigidity and is represented by \(G\).
$$ \tau = G \gamma $$
Again to obtain the convenient form of this Law, we can substitute the \(\tau\) with the \(V/A_s\) and shearing strain \(\gamma\) with the \(\Delta_s/L\).
$$ \Delta_s=\frac{VL}{A_sG} $$
Limitations of Hooke’s law
The above equations are the relationships among the total elongation \(\Delta L \& (\Delta_s)\), force applied \(P\&(V)\), total length \(L\), the cross-sectional area \(A\&(A_s)\) and modulus of elasticity \(E\) and modulus of rigidity \(G\). The relation, which seems so simple, comes with some restrictions or, we can say, assumptions while defining the relations. Like when we say \(\sigma = \frac{P}{A} \& \tau=\frac{V}{A_s}\) we assume that the stress is uniformly distributed in the cross-section and load is axial (tangential for shear )and constant throughout the length and the member (bar) has constant cross-section throughout the length. Most importantly, the stress in the material is below the proportional limit.
Conclusions
Hooke’s Law is the fundamental building block while learning the strength of the material. This concept is further used for the validity of the Principle of Superposition (Link). Modulus of elasticity, modulus of rigidity are elastic constant. Do they have relations or they are independent of each other?
Some key learning from the post:
- Hooke’s Law states that stress is directly proportional to strain.
- Young’s modulus is the proportionality constant, later known as the modulus of elasticity.
- Modulus of elasticity is used for axial tension case and is defined as the ratio of stress to strain.
- Modulus of rigidity is the modulus of elasticity in shear. It can be defined as shear stress to shear strain.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.