Before moving into the design procedure of a R.C.C beams you should be aware about the different types of beams available. There are basically seven types of beam depending upon the support and geometry of the beam section, they are:
- Simply supported beam
- Fixed beam
- Overhanging beam
- Double over hanging beam
- Continuous beams
- Cantilever beams
- Trussed beams
Check this post to know more about these beams
The design procedure of each beam is different only the underlying principle is the same. In this post I will explain about the step by step procedure of design of a simply supported beam, by considering an example problem.
Problem Statement : Design a beam, which is simply supported at both ends. Assume effective cover = 40 mm and use M20 concrete and Fe415 steel.
Given data as per the design problem:
- span (L) = 2.5 m
- breadth (b) = 230 mm
- Depth (D) = 380 mm
- effective cover = 40 mm
- d = 380 – 40 = 340 mm
- fck = 20 N/ mm2
- fy =415 N/ mm2
Analysis of the section
In this step, compute the moment of the beam.
Consider the various loads due to
- Load from stair flights: Landing of stair flights, $w_l = 12.45 kN/m^2, L = 3.26 m$ , $$w_l = 12.45 \times \frac{3.26}{2} = 20.3 kN/m$$
- Load from grill 4.8 m high $4.8 \times 1.25 = 6.0 kN/m$
- Self weight: $ 25 \times 0.23 \times (0.38 – 0.1 ) = 1.6 kN/m$
- Total working load = $w = 27.9 kN/m$
- Design ultimate load = $w_u = 1.5 \times 27.9 = 41.9 kN/m$
Design Moment : $M_u = w_u L^2/ 8 = 32.7 kNm$
Max. ultimate moment of resistance: $M_{ur.max} = R_{u.max}bd^2 = 2.76 \times 230 \times 340^2 \times 10^{-6} = 73.4 kNm > M_u$.
Therefore for this case Mur,max> Mu ; so it is a under reinforced beam section.
Calculate the area of reinforcement (Ast)
Depending on the type of beam cal. area of steel at mid -span, For this section, Required:
$$
A_{s t}=\frac{0.5 f_{c k}}{f_y}\left[1-\sqrt{1-\frac{4.6 M_u}{f_{c k} b d^2}}\right] \times b \times d
$$
$$
A_{s t}=\frac{0.5 \times 20}{415}\left[1-\sqrt{1-\frac{4.6 \times 32.7 \times 10^6}{20\times 230 \times 340^2}}\right] \times 230 \times 340
$$
$$
A_{s t}= 289 mm^2 $$
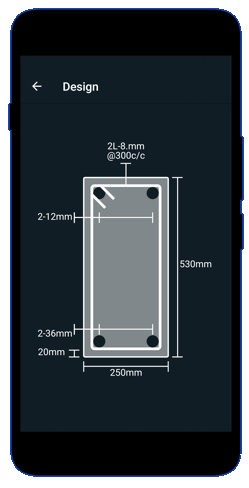
Provide 3 bars of 12 mm dia. in the bottom of the beam, where 2 bars on the middle of the beam and 1 bar from 0.5 m from support.
Provide 2 bars of 10 mm dia as anchor bars, that is satisfying the minimum reinf. condition in the top of the beam section.
Design for shear
$$
V_{u \max }=w_u L / 2=41.9 \times 2.5 / 2=52.4 \mathrm{kN} \text {. }
$$
$V_{u c}=\tau_{u c} b d, \tau_{u c}$ depends upon $p_t \%$ at support.
$A_{s t 1}=2 $ bars of $\# 12 \mathrm{~mm}=2 \times 113=226 \mathrm{~mm}^2$ (tension steel at support)
$$
p_t=100 \times 226 /(230 \times 340)= 0.289 \%
$$
$$
\begin{aligned}
\tau_{u c} & =0.36+\frac{(0.48-0.36)}{(0.50-0.25)} \times(0.289-0.25)=0.3787 \mathrm{~N} / \mathrm{mm}^2 \\
V_{u c} & =0.3787 \times 230 \times 340 / 1000= 29.61 \mathrm{kN} \\
V_{usv.min } & =0.4 \mathrm{bd}=0.4 \times 210 \times 345 / 1000= 31.28 \mathrm{kN} \\
V_{u r. \text { min }} & = 29.61 + 31.26 = 60.87 \mathrm{kN}>V_{u \text { max }}(= 52.4 \mathrm{kN}) \\
& \therefore \text { Minimum stirrups are sufticient. }
\end{aligned}
$$
Provide 2 legged stirnups $\left(A_{s t}=100.53\mathrm{~mm}^2\right)$
Pitch $\quad s=0.87 f_y a_{s t} /(0.4 b)=0.87 \times 415\times 100/( 0.4 \times 230)= 394.5 \mathrm{~mm}$ Say $390 \mathrm{~mm}>.75 \times 340$ and $<300 \mathrm{~mm} \quad \therefore \mathrm{O} . \mathrm{K}$.
Provide $\phi 8 \mathrm{~mm} 2$- legged stirrups @ 250mm c/c
Different checks of a R.C.C beam as per IS 456: 2000.
Check for effective cover: For mild environment nominal cover = 20 mm
$$d’ = \text{Nominal cover} + \text{dia. of stirrups } + \text{dia. of main bars}$$
$$d’ = 20 + 6 + 12/2 = 32 mm < 40 mm , \text{Hence O.K.} $$
Check for Deflection:
$$
\begin{aligned}
f_s & =0.58 \times 415 \times 289 / 339=205 \mathrm{~N} / \mathrm{mm}^2 \\
\left(p_t\right)_{\text {prov }} & =100 \times 339 /(230 \times 340)= 0.43 \% \\
\text { For } f_s & =205 \mathrm{Nimm}^2 \text { and } p_t= 0.43 \%, \quad \alpha_t=1.5
\end{aligned}
$$
Basic L/d ratio = 20 for simply supported beams,
Required d = 250/ (20* 1.5) = 84 mm << 340 mm… Hence Safe.
Check for Development length:
Required $\quad L_d=47 \phi=47 \times 12=564 \mathrm{~mm}$
Now , $M_1=M \cdot R$. of $A_{s t 1}$ at support , $A_{st \prime}=2-\# 12=226 \mathrm{~mm}^2$
$$
\begin{aligned}
& M_1=0.87 \times 415 \times 226 \times 340\left(1-\frac{415 \times 226}{20 \times 230 \times 340}\right) \times 10^{-6} \\
& =26.1 \mathrm{kN} . \mathrm{m} \\
r & =V_{u \cdot \max }=52.4 \mathrm{kN} . \\
L_o & =L_d / 3-b_s / 2 \quad \text { where, } b_s=\text { vidth of support } \\
\text { Assuming } b_s & =230 \mathrm{~mm}, \quad L_o=564 / 3-230 / 2=73 \mathrm{~mm} . \\
\text { Available } L_d & =\frac{1.3 M_1}{v}+L_o=\frac{1.3 \times 26.1 \times 1000 }{52.4}+ 73= 720 \mathrm{~mm} \\
& \therefore 564 \mathrm{~mm}<720 \mathrm{~mm} \therefore \text { safe. }
\end{aligned}
$$
Conclusions
In this blog post, we have delved into a practical problem that provides an explanation of a SRB. As per IS:456:2000, Indian Standards, we have designed a simply supported rectangular beam section.
So, let us discuss the key points from this problem as follows:
- Significance of Design and Analysis: It gives the need to consider various factors, including load distribution, and reinforcement to ensure the function of a beam.
- Consideration of Critical Factors: Throughout our design procedure, we have discussed significant factors such as bending moments, shear forces, and deflection limits.
- Integration of Theory and Practice: All in one, by following the reinforcement detailing guidelines as per Indian codes, engineers can develop structurally sound and efficient solutions that meet safety and performance criteria.
Do check this post to know the design procedure for a DRB.
Beam design
- RCC Beam Design is a free app for designing reinforced concrete beams as per Indian Standards.
- RCC Design and detailing could be performed by Limit State Method specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


