Isothermal is a process in which the temperature doesn’t change. The simpler it sounds, the more difficult it is to produce them in real life. Despite adding heat, the temperature doesn’t change for such a process. Why that happens and what is the significance of these processes you will see in this post that begins by explaining the isothermal process in detail.
Isothermal process
An isothermal process is a thermodynamic process in which the system’s temperature remains constant. The system can perform work and heat transfer through its boundaries. But these events won’t change the overall temperature of the system. Something within the system works to maintain this constant temperature.
There are two broader possibilities for ideal gases that can make their system isothermal:
- No heat and no work: Such a case when neither heat is transferred, nor work is done by the system. In such cases, the change in internal energy and, as a result, the temperature remains zero. That leads to isothermal behavior. But, in this case, there is no change in system properties. It can’t be considered a process. An example of this is fluid inside a thermo-flask.
- Heat transfer and work done: To maintain the internal energy of the system constant, if heat is added, then work needs to be done by the system, and vice-versa. This leads to an isothermal process, these scenarios happen during the phase change like evaporation or melting. The presence of only one (heat or work) will lead to a change in the system’s internal energy and will lead to a change in temperature.
Work done in Isothermal process
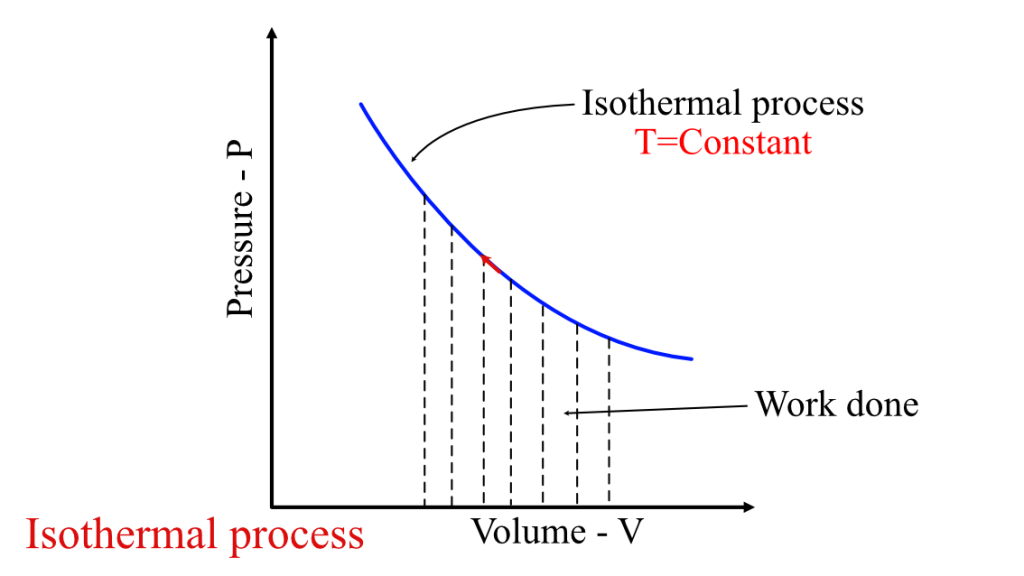
The work is represented in terms of P-dV work for a closed system undergoing this process. And for a system having ideal gas as the working substance, the work done becomes:
$$W = nRT\ln(\frac{V_f}{V_i})$$
Where n, R, and T are the molar number, Universal gas constant, and temperature, respectively. Vf and Vi represent the final and initial volume of the system in the process.
Graphically, it is represented as the area under the isotherm in the P-V diagram, as shown in the figure below. An isotherm is any curve or contour having a constant temperature.
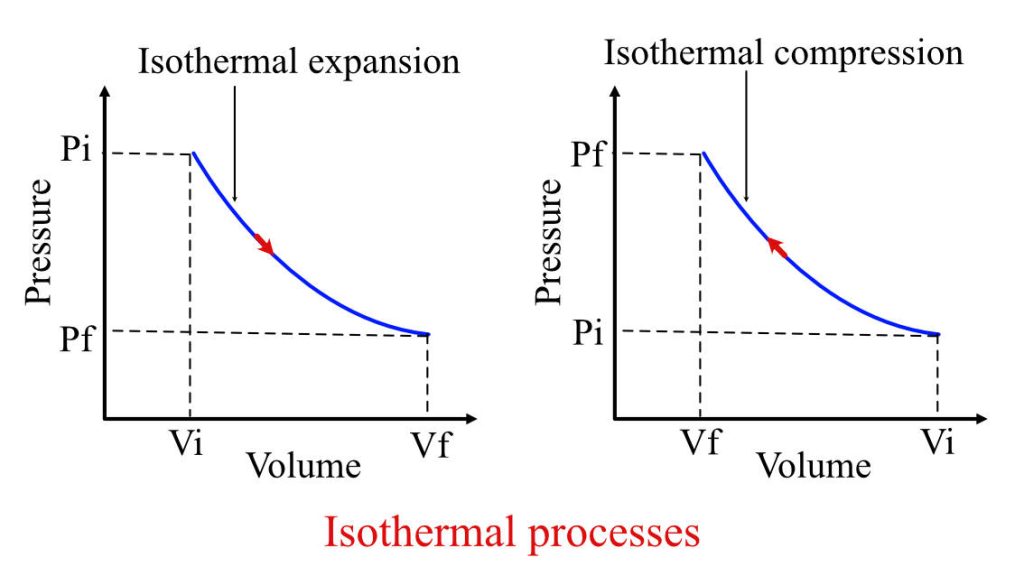
Isothermal expansion & Isothermal compression process
There is a common misconception that when there is heat addition in the system, then the temperature will change. Isothermal process breaks this misconception. During the isothermal compression or expansion process, the net effect of the compression or expansion is balanced by heat transfer from the system. Thus, maintaining the system’s temperature constant throughout the process.
Graphically these two processes look identical, just with a change in direction, as shown below.
Isothermal process and First Law of Thermodynamics
Every system, including living organisms and non-living objects, obeys the law of nature, including the First law of Thermodynamics. For a system undergoing this process, the First law of Thermodynamic implementation gives “The net effect of work done will be equal to net heat transfer.”
The above statement can be easily derived by taking the classical differential form of the First law for a closed system, which is:
$$dU = dQ- dW$$
where dU is the change in internal energy. dQ and dW are the net heat transfer and work done.
For an ideal gas, the system’s energy is only a function of temperature. Thus, internal energy change becomes zero. This leads to the following:
$$dQ = dW$$
Boyle’s law
The behavior of gases under different conditions has been studied by many scientists. Their discoveries led to well-known laws of gases. Once such a law is defined for the gases changing at a constant temperature.
In the 17th century, Robert William Boyle formulated this law that defines the relationship between pressure and volume at a constant temperature. It states, ” For a fixed mass of gas at a constant temperature, the volume & pressure follows inverse relation.”
Mathematically, it becomes
$$PV = \text{ Constant}$$
Interestingly, this relation PV= Constant also holds for ideal gases undergoing the isothermal process.
Examples of Isothermal process
In nature, you can find many processes going unnoticed. This process can occur in a system as minute as cells to as enormous as clouds.
A few of the isothermal processes happening in nature are:
- Phase change: All the phase change, whether ice to water, water to steam, or melting of metals, happens at constant temperatures.
- Carnot cycle and Rankine cycle: Heat exchange occurs isothermally in both these and many more thermodynamic cycles.
- Refrigerators and heat pump: Of the many processes happening inside refrigerators and heat pump, there are processes like heat addition and heat rejection that occurs isothermally in them.
Conclusions
The Isothermal process is a combination of heat and work transfer combined. Apart from phase change, it is hard to achieve these processes in practical applications. In steam engines and refrigerators, it is applied where the phase change of refrigerant or fluid occurs; that is the closest we have.
Some key learnings from the post:
- Isothermal process: An isothermal process is a thermodynamic process in which the system’s temperature remains constant.
- Isothermal expansion and compression process: During the isothermal compression or isothermal expansion process, the net effect of the compression or expansion is balanced by heat transfer from the system.
- First law implementation for the Isothermal process: The net effect of work done will equal net heat transfer.
- Boyle’s law: For a fixed mass of gas at a constant temperature, the volume & pressure follows an inverse relation.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.